Multiple Choice
Select the parametric equations matching with the following graph. 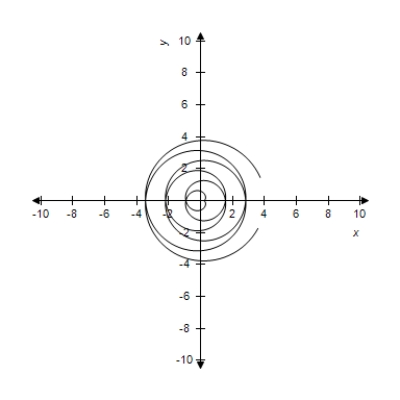
A) Involute of circle:
B) Involute of circle:
C) Involute of circle:
D) Involute of circle:
E) Involute of circle:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q104: Find the standard form of the equation
Q431: Eliminate the parameter and write the
Q432: Identify the conic as a circle
Q434: Find the standard form of the
Q435: Find the standard form of the
Q437: Identify the conic and select its
Q438: As a speeding train crosses a
Q439: A point in rectangular coordinates is
Q440: Give the coordinates of the circle's
Q441: Select the curve represented by the