Solved

A Box Contains 7 Red Balls, 6 White Balls, and 3

Question 5

Multiple Choice

A box contains 7 red balls, 6 white balls, and 3 black balls. Two balls are drawn at random from the box without replacement of the first before the second is drawn. What is the probability of getting a red R ball on the first draw and a white W ball on the second? ​


A) Pr(R first ∩ W second) = A box contains 7 red balls, 6 white balls, and 3 black balls. Two balls are drawn at random from the box without replacement of the first before the second is drawn. What is the probability of getting a red R ball on the first draw and a white W ball on the second? ​ A) Pr(R first ∩ W second) = B) Pr(R first ∩ W second) = C) Pr(R first ∩ W second) = D) Pr(R first ∩ W second) = E) Pr(R first ∩ W second) =
B) Pr(R first ∩ W second) = A box contains 7 red balls, 6 white balls, and 3 black balls. Two balls are drawn at random from the box without replacement of the first before the second is drawn. What is the probability of getting a red R ball on the first draw and a white W ball on the second? ​ A) Pr(R first ∩ W second) = B) Pr(R first ∩ W second) = C) Pr(R first ∩ W second) = D) Pr(R first ∩ W second) = E) Pr(R first ∩ W second) =
C) Pr(R first ∩ W second) = A box contains 7 red balls, 6 white balls, and 3 black balls. Two balls are drawn at random from the box without replacement of the first before the second is drawn. What is the probability of getting a red R ball on the first draw and a white W ball on the second? ​ A) Pr(R first ∩ W second) = B) Pr(R first ∩ W second) = C) Pr(R first ∩ W second) = D) Pr(R first ∩ W second) = E) Pr(R first ∩ W second) =
D) Pr(R first ∩ W second) = A box contains 7 red balls, 6 white balls, and 3 black balls. Two balls are drawn at random from the box without replacement of the first before the second is drawn. What is the probability of getting a red R ball on the first draw and a white W ball on the second? ​ A) Pr(R first ∩ W second) = B) Pr(R first ∩ W second) = C) Pr(R first ∩ W second) = D) Pr(R first ∩ W second) = E) Pr(R first ∩ W second) =
E) Pr(R first ∩ W second) = A box contains 7 red balls, 6 white balls, and 3 black balls. Two balls are drawn at random from the box without replacement of the first before the second is drawn. What is the probability of getting a red R ball on the first draw and a white W ball on the second? ​ A) Pr(R first ∩ W second) = 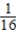B) Pr(R first ∩ W second) = 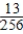C) Pr(R first ∩ W second) = 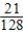D) Pr(R first ∩ W second) = 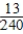E) Pr(R first ∩ W second) =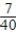

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: Suppose that five of the eight students

Q2: A box of 27 transistors contains 7

Q3: In a certain city, the Democratic, Republican,

Q4: An automatic teller machine requires that each

Q6: A bag contains 9 white balls and

Q7: Suppose a fair coin is tossed 6

Q8: A retailer purchases 140 of a new

Q9: An urn contains 4 red, 7 white,

Q10: A card is drawn from an ordinary

Q11: To see whether a bank has enough