Multiple Choice
In a certain city, the Democratic, Republican, and Consumer parties always nominate candidates for mayor. The probability of winning in any election depends on the party in power and is given by the following transition matrix. 
Using the given transition matrix and assuming the initial-probability vector is 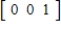 , find the probability vector for the fourth stage of the Markov chain. (This initial-probability vector indicates that a Consumer is certain to win the initial election.)
, find the probability vector for the fourth stage of the Markov chain. (This initial-probability vector indicates that a Consumer is certain to win the initial election.)
A) 
B) 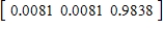
C) 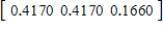
D) 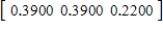
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Suppose that five of the eight students
Q2: A box of 27 transistors contains 7
Q4: An automatic teller machine requires that each
Q5: A box contains 7 red balls, 6
Q6: A bag contains 9 white balls and
Q7: Suppose a fair coin is tossed 6
Q8: A retailer purchases 140 of a new
Q9: An urn contains 4 red, 7 white,
Q10: A card is drawn from an ordinary
Q11: To see whether a bank has enough