The Owner of a Stationary and Office Supplies Online Store

Multiple Choice

The owner of a stationary and office supplies online store is interested in whether the day of the week affects the number of visitors who made purchases. The null hypothesis is that the number of buyers does not depend on the weekday. Throughout the week the number of buyers was counted. Minitab was used to perform a chi-square goodness-of-fit test for these data. Using the Minitab output and a significance level of α = 0.1, determine the P-value and carry out a test of the null hypothesis. ​ ​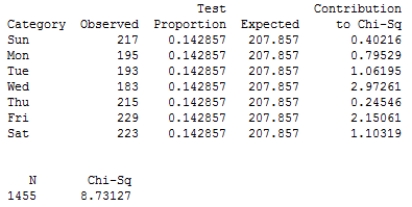

A) 0.030 < P-value < 0.035, thus the null hypothesis is rejected. There is convincing evidence that the number of buyers depends on the weekday.
B) 0.045 < P-value < 0.050, thus the null hypothesis is rejected. There is no convincing evidence that the number of buyers depends on the weekday.
C) P-value < 0.001, thus the null hypothesis is rejected. There is convincing evidence that the number of buyers depends on the weekday.
D) 0.095 < P-value < 0.100, thus the null hypothesis is not rejected. There is convincing evidence that the number of buyers depends on the weekday.
E) 0.1 < P-value, thus the null hypothesis is not rejected. There is no convincing evidence that the number of buyers depends on the weekday.