Multiple Choice
Set up the three-dimensional integral where R is the "ice-cream cone" enclosed by a sphere of radius 2 centered at the origin and the cone .Use rectangular coordinates. 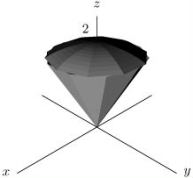
A)
B)
C)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q60: Calculate the following integral exactly.(Your answer
Q61: Evaluate the integral <span class="ql-formula"
Q62: Let x and y have joint
Q63: Set up (but do not evaluate)an
Q64: A solid is bounded below by
Q66: Let R be the region bounded
Q67: Find the mass of the solid
Q68: Compute the area of the flower-like
Q69: The joint density function for random
Q70: Upper and lower sums for a