Multiple Choice
The region W is shown below.Write the limits of integration for in spherical coordinates. 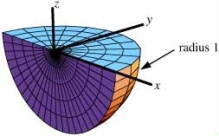
A)
B)
C)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q17: Calculate the following integral exactly.(Your answer
Q18: Suppose a solid is the region
Q19: A cylindrical tube of radius 2cm and
Q20: Let R be the region in
Q21: Evaluate the integral <span class="ql-formula"
Q23: Evaluate exactly the integral <span
Q24: Set up an iterated integral for
Q25: Evaluate <span class="ql-formula" data-value="\int _
Q26: Let W be the region between
Q27: Estimate <span class="ql-formula" data-value="\int"><span class="katex"><span