The Function H(x)is a Continuous Differentiable Function Whose Graph Is

Multiple Choice

The function h(x) is a continuous differentiable function whose graph is drawn below.The accompanying table provides some information about h(x) and its derivatives. 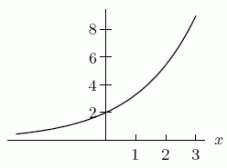$$\begin{array} { c c c c c } \boldsymbol { x } & \boldsymbol { h } ( \boldsymbol { x } ) & \boldsymbol { h } ^ { \prime } ( \boldsymbol { x } ) & \boldsymbol { h } ^{ { \prime }{ \prime }} ( \boldsymbol { x } ) & \boldsymbol { h } ^ {{ \prime }{ \prime } { \prime } } ( \boldsymbol { x } ) \\0 & 2 & 1 & 0.50 & 0.25 \\1 & 3.29 & 1.64 & 0.82 & 0.41 \\2 & 5.43 & 2.71 & 1.35 & 0.67 \\3 & 8.96 & 4.48 & 2.24 & 1.12\end{array}$$ h(x) , h'(x) , h"(x) and h"'(x) are all increasing functions.Suppose we use a tangent line approximation at zero to approximate h(0.1) .Find a good upper bound for the error.

A) 0.0025
B) 0.0820
C) 0.1066
D) 0.1558