Consider the Ellipse Pictured Below: the Perimeter of the Ellipse

Short Answer

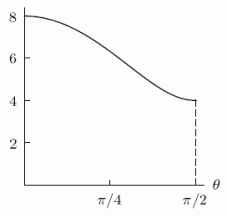Consider the ellipse pictured below: The perimeter of the ellipse is given by the integral $\int_{0}^{\pi / 2} 8 \sqrt{1-\frac{3}{4} \sin ^{2} \theta} d \theta$ .It turns out that there is no elementary antiderivative for the function $f(\theta)=8 \sqrt{1-\frac{3}{4} \sin ^{2} \theta}$ , and so the integral must be evaluated numerically.A graph of the integrand f( $\theta$ )is shown below. Calculate the right sum that approximates the definite integral with N = 4 equal divisions of the interval.Round to 4 decimal places.