Consider a Continuous Function with the Following Properties $f(0)=4$ $\left|f^{\prime}(x)\right|<0.5$ $f^{\prime \prime}(x)<0$

Multiple Choice

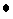
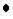
Consider a continuous function with the following properties: 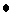$f(0) =4$ $\left|f^{\prime}(x) \right|<0.5$ $f^{\prime \prime}(x) <0$ for $x<0$ $f^{\prime}(1) =0$ . Which of the following is true?

A) The graph must have a local maximum for $x<0$ .
B) The graph must not have a local maximum for $x<0$ .
C) The graph may or may not have a local maximum for $x<0$ .