Short Answer
A single cell of a bee's honey comb has the shape shown.The surface area of this cell is given by where h, s, are as shown in the picture.Keeping h and s fixed, for what angle, , is the surface area minimal? Round to the nearest one tenth of a degree. 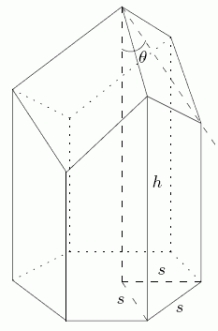
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q54: Consider a continuous function with the
Q55: Let <span class="ql-formula" data-value="f(x)=e^{\frac{-x^{2}}{b}}"><span class="katex"><span
Q56: A submarine can travel 30mi/hr submerged and
Q57: A cupful of olive oil falls
Q58: One fine day you take a
Q60: Consider the two-parameter family of curves
Q61: A lady bug moves on the
Q62: Consider the function <span class="ql-formula"
Q63: Below is the graph of the rate
Q64: A window with a rectangular base is