Solve the Absolute Value Inequality $\phi$ , Use Interval Notation to Express the Solution Set and Use

Multiple Choice

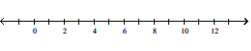
Solve the absolute value inequality. Other than $\phi$ , use interval notation to express the solution set and graph the solution set on a number line.
- $|3 x-4|+1>-8$

A) $\left(-\frac{5}{3}, \infty\right)$

B) $(-\infty, \infty)$

C) $\left(-\frac{5}{3}, \frac{13}{3}\right)$

D) $\varnothing$