After Analyzing the Age-Earnings Profile for 1,744 Workers as Shown

Essay

After analyzing the age-earnings profile for 1,744 workers as shown in the figure, it
becomes clear to you that the relationship cannot be approximately linear. 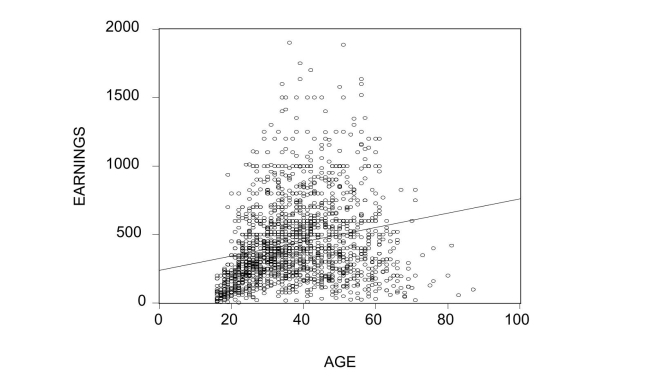You estimate the following polynomial regression model, controlling for the effect of
gender by using a binary variable that takes on the value of one for females and is zero
otherwise: $\begin{aligned}\widehat{\text { Earn }}= & -795.90+82.93 \times \text { Age }-1.69 \times A g e^{2}+0.015 \times A g e^{3}-0.0005 \times \text { Age }^{4} \\& (283.11)(29.29) \quad(1.06) \quad(0.016) \\\\& -163.19 \text { Female, } R^{2}=0.225, \text { SER }=259.78 \\& (12.45)\end{aligned}$ (a) Test for the significance of the $A _ { g e } e ^ { 4 }$ coefficient. Describe the general strategy to determine the appropriate degree of the polynomial.