Solve Using Cramer's Rule $W _ { 1 }$ And $W _ { 2 }$

Multiple Choice

Solve using Cramer's Rule.
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If a force of 124 pounds is applied at the peak of the truss, then the forces or weights $W _ { 1 }$ and $W _ { 2 }$ exerted parallel to each rafter of the truss are determined by the following linear system of equations. Solve the system to find 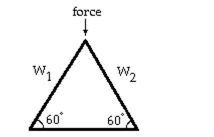$W _ { 1 }$ and $W _ { 2 }$ .


$$\begin{array} { l } \frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 124 \\W _ { 1 } - W _ { 2 } = 0\end{array}$$

A) $\mathrm { W } _ { 1 } = - 71.59 \mathrm { lb } ; \mathrm { W } _ { 2 } = - 71.59 \mathrm { lb }$
B) $\mathrm { W } _ { 1 } = 71.59 \mathrm { lb } ; \mathrm { W } _ { 2 } = 71.59 \mathrm { lb }$
C) $\mathrm { W } _ { 1 } = 71.59 \mathrm { lb } ; \mathrm { W } _ { 2 } = 62 \mathrm { lb }$
D) $\mathrm { W } _ { 1 } = 41.33 \mathrm { lb } ; \mathrm { W } _ { 2 } = 41.33 \mathrm { lb }$