Solve the System to Find $$W _ { 1 } \text { and } W _ { 2 }$$

Multiple Choice

Solve the system to find $$W _ { 1 } \text { and } W _ { 2 }$$
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type 223) of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If
A force of 116 pounds is applied at the peak of the truss, then the forces or weight $$\mathrm { W } _ { 1 } \text { and } \mathrm { W } _ { 2 }$$ exerted parallel to each rafter of the truss are determined by the following linear system of equations.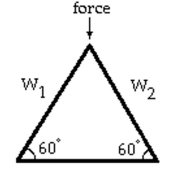

$$\begin{array} { l } \frac { \sqrt { 3 } } { 2 } \left( W _ { 1 } + W _ { 2 } \right) = 116 \\W _ { 1 } - W _ { 2 } = 0\end{array}$$

A) $W _ { 1 } = 66.97 \mathrm { lb } ; W _ { 2 } = 66.97 \mathrm { lb }$
B) $\mathrm { W } _ { 1 } = 38.67 \mathrm { lb } ; \mathrm { W } _ { 2 } = 38.67 \mathrm { lb }$
C) $W _ { 1 } = - 66.97 \mathrm { lb } ; W _ { 2 } = - 66.97 \mathrm { lb }$
D) $\mathrm { W } _ { 1 } = 66.97 \mathrm { lb } ; \mathrm { W } _ { 2 } = 58 \mathrm { lb }$