Solve the System to Find $$W _ { 1 } \text { and } W _ { 2 }$$

Multiple Choice

Solve the system to find $$W _ { 1 } \text { and } W _ { 2 }$$
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If
A 172-pound force is applied at the peak of the truss, then the forces or weights W $$\mathrm { W } _ { 1 } \text { and } \mathrm { W } _ { 2 }$$ exerted
Parallel to each rafter of the truss are determined by the following linear system of equations.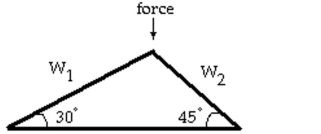
$\begin{array}{l}W_{1}+\sqrt{2} W_{2}=344 \\\sqrt{3} W_{1}-\sqrt{2} W_{2}=0\end{array}$

A) $\mathrm { W } _ { 1 } = 154.21 \mathrm { lb } ; \mathrm { W } _ { 2 } = 125.91 \mathrm { lb }$
B) $\mathrm { W } _ { 1 } = 125.91 \mathrm { lb } ; \mathrm { W } _ { 2 } = 154.21 \mathrm { lb }$
C) $W _ { 1 } = 62.96 \mathrm { lb } ; W _ { 2 } = 77.11 \mathrm { lb }$
D) $W _ { 1 } = 172 \mathrm { lb } ; W _ { 2 } = 210.66 \mathrm { lb }$