Multiple Choice
Graph the exponential function using transformations where appropriate.
- 
A) 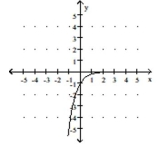
B) 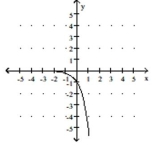
C) 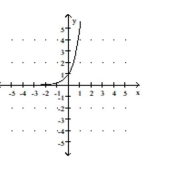
D) 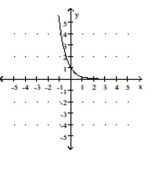
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q148: Round your answer to the nearest
Q149: Use properties of logarithms to evaluate
Q150: rite the word or phrase that
Q151: Find the value. Give an approximation
Q152: Round your answer to the nearest
Q154: Graph the function. Give the domain
Q155: If the function is one-to-one, find
Q156: Choose the one alternative that best
Q157: Use a graphing calculator to estimate
Q158: Use the properties of logarithms to