Multiple Choice
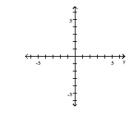
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
- 
A) 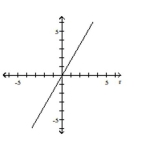
B) 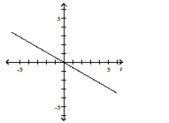
; line through the pole making an angle of with the polar axis
C) 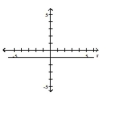
; line through the pole making an angle of with the polar axis
D) 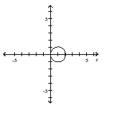
horizontal line units below the pole
center at in rectangular coordinates
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q39: Choose the one alternative that best
Q40: Plot the point given in polar
Q41: Find the angle between v and
Q42: Use the given vectors to find
Q43: Plot the complex number in the
Q45: Plot the point given in polar
Q46: Decompose v into two vectors v1
Q47: Choose the one alternative that best
Q48: Find the dot product v ·
Q49: Find the indicated cross product.<br>- <span