Multiple Choice
Graph Ellipses Not Centered at the Origin
- 
A) 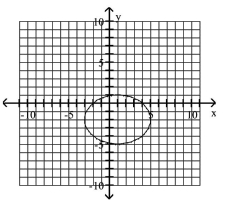
B) 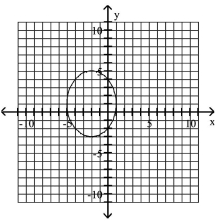
C) 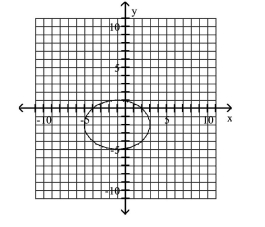
D) 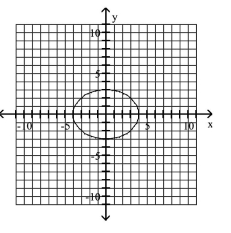
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q69: Convert the equation to the standard
Q70: Rotation of Axes<br>1 Identify Conics Without
Q71: Find the standard form of the
Q72: Graph the ellipse and locate the
Q73: Rotation of Axes<br>1 Identify Conics Without
Q75: Eliminate the Parameter<br>- <span class="ql-formula" data-value="x
Q76: Graph the ellipse and locate the
Q77: Rotation of Axes<br>1 Identify Conics Without
Q78: Additional Concepts<br>- <span class="ql-formula" data-value="y ^
Q79: Eliminate the Parameter<br>-An ellipse: <span