Multiple Choice
Graph the Polar Equations of Conics
- Identify the directrix and vertex.
A) directrix: 1 unit(s) to the left of
the pole at
vertex: 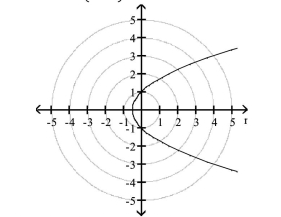
B) directrix: 1 unit(s) to the right of
the pole at
vertex: 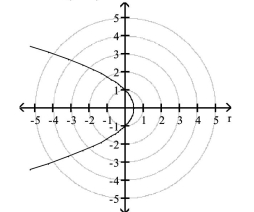
C) directrix: 1 unit(s) above
the pole at
vertex: 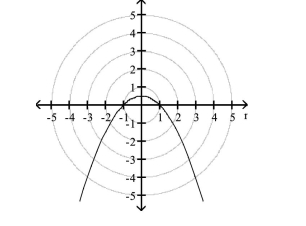
D) directrix: 1 unit(s) below
the pole at
vertex: 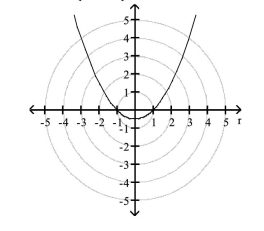
Correct Answer:

Verified
Correct Answer:
Verified
Q137: Graph the parabola with the given
Q138: Tech: Parametric Equations<br>-Cycloid: <span class="ql-formula"
Q139: Find the standard form of the
Q140: The Parabola<br>1 Graph Parabolas with Vertices
Q141: Rotation of Axes<br>1 Identify Conics Without
Q143: Graph Parabolas with Vertices Not at
Q144: Find the solution set for the
Q145: Eliminate the Parameter<br>- <span class="ql-formula" data-value="\mathrm
Q146: Identify Conics Without Rotating Axes<br>- <span
Q147: Graph the ellipse and locate the