Multiple Choice
Graph the Polar Equations of Conics
- Identify the directrix and vertex.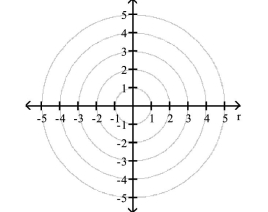
A) directrix: 3 unit(s) above
the pole at
vertex: 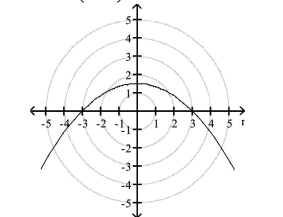
B) directrix: 3 unit(s) to the right of
the pole at
vertex: 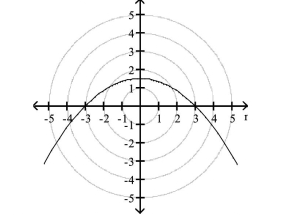
C) directrix: 3 unit(s) to the left of the pole at
vertex: 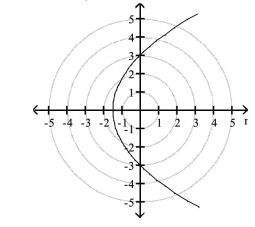
D) directrix: 3 unit(s) below
the pole at
vertex: 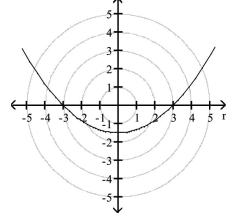
Correct Answer:

Verified
Correct Answer:
Verified
Q5: Match the equation to the graph.<br>-
Q6: Graph the parabola.<br>- <span class="ql-formula" data-value="x
Q7: Graph the Polar Equations of Conics<br>-
Q8: Identify Conics Without Rotating Axes<br>- <span
Q9: Use Rotation of Axes Formulas<br>- <span
Q11: Graph the ellipse and locate the
Q12: Write Equations of Parabolas in Standard
Q13: Identify Conics Without Rotating Axes<br>- <span
Q14: Additional Concepts<br>- <span class="ql-formula" data-value="x ^
Q15: Solve Applied Problems Involving Parabolas<br>-An experimental model