Multiple Choice
Tech: Conic Sections in Polar Coordinates
- 
A) 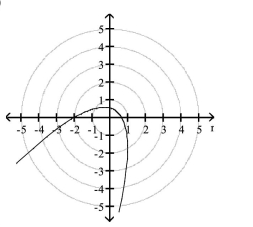
B) 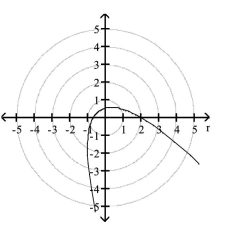
C) 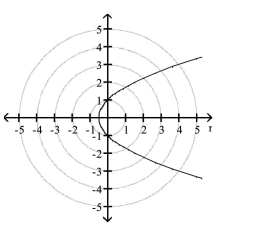
D) 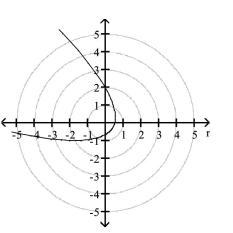
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q37: Use Rotation of Axes Formulas<br>- <span
Q38: Write the appropriate rotation formulas so
Q39: Use Rotation of Axes Formulas<br>- <span
Q40: Write Equations of Hyperbolas in Standard
Q41: Write Equations of Parabolas in Standard
Q43: Graph Ellipses Not Centered at the
Q44: Eliminate the Parameter<br>- <span class="ql-formula" data-value="\mathrm
Q45: Graph Parabolas with Vertices Not at
Q46: Understand the Advantages of Parametric Representations<br>-Ron
Q47: Graph the ellipse and locate the