Solve the System to Find $W _ { 1 } \text { and } W _ { 2 }$

Multiple Choice

Solve the system to find $W _ { 1 } \text { and } W _ { 2 }$
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If a 123-pound force is applied at the peak of the truss, then the forces or weights $W _ { 1 }$ and $W _ { 2 }$ exerted parallel to each rafter of the truss are determined by the following linear system of equations.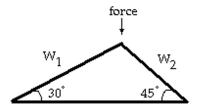


$$\begin{array} { l } W _ { 1 } + \sqrt { 2 } W _ { 2 } = 246 \\\sqrt { 3 } W _ { 1 } - \sqrt { 2 } W _ { 2 } = 0\end{array}$$

A) $\mathrm { W } _ { 1 } = 110.28 \mathrm { lb } ; \mathrm { W } _ { 2 } = 90.04 \mathrm { lb }$
B) $\mathrm { W } _ { 1 } = 90.04 \mathrm { lb } ; \mathrm { W } _ { 2 } = 110.28 \mathrm { lb }$
C) $\mathrm { W } _ { 1 } = 123 \mathrm { lb } ; \mathrm { W } _ { 2 } = 150.64 \mathrm { lb }$
D) $W _ { 1 } = 45.02 \mathrm { lb } ; W _ { 2 } = 55.14 \mathrm { lb }$