Related Questions
Q125: Given <span class="ql-formula" data-value="f (
Q126: Give the domain and range.<br>- <span
Q127: Let <span class="ql-formula" data-value="\mathrm {
Q128: Use the graph of f to sketch
Q129: Solve the equation.<br>- <span class="ql-formula" data-value="\left(
Q131: Solve the equation and express the
Q132: Graph the exponential function using transformations where
Q133: If <span class="ql-formula" data-value="f (
Q134: Use the definition of inverses to
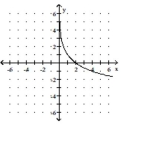
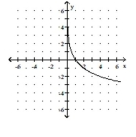
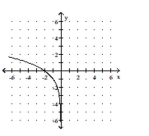
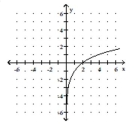
Q135: Match the function with its graph.<br>-