Multiple Choice
Give a rule for the piecewise-defined function. Then give the domain and range.
-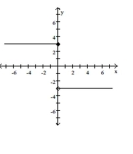
A) Domain: , Range:
B) ; Domain: , Range:
C) ; Domain: , Range:
D) ; Domain: , Range:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q166: Determine if the function is even,
Q167: Graph the equation by plotting points.<br>-
Q168: Find the center-radius form of the
Q169: Use the graphs to find the
Q170: Find the slope and the y-intercept
Q172: Consider the function h as defined.
Q173: Find the coordinates of the other
Q174: A new chocolate company is estimating
Q175: Graph the circle.<br>- <span class="ql-formula" data-value="x^{2}+(y-5)^{2}=9"><span
Q176: Graph the point symmetric to the given