Multiple Choice
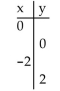
Complete the ordered pairs. Then graph the equation.
- 
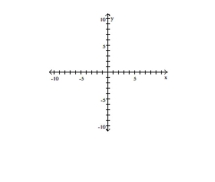
A) 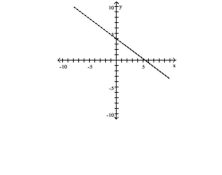
B) 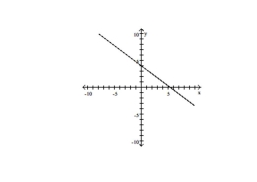
C) 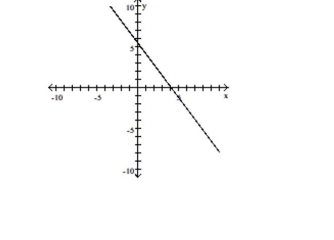
D) 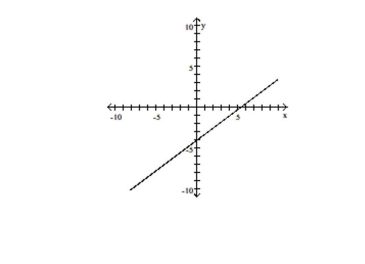
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q84: Find the y- and x-intercepts for
Q85: Graph the circle.<br>- <span class="ql-formula" data-value="(x-4)^{2}+y^{2}=25"><span
Q86: In 1980, the population of a
Q87: <span class="ql-formula" data-value="\text { The circle with
Q88: Choose one of the four lines graphed
Q90: Identify whether the slope is positive, negative,
Q91: Find the average rate of change.
Q92: Choose one of the four lines
Q93: Decide whether the statement is true or
Q94: Use this graph to answer the question.<br><img