Transform the Polar Equation to an Equation in Rectangular Coordinates $$r \sec \theta = - 6$$

Multiple Choice

Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
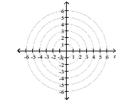
- $$r \sec \theta 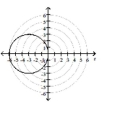= - 6$$

A)

$( x + 3 ) ^ { 2 } + y ^ { 2 } = 9$ ; circle, radius 3
center $( - 3,0 )$ in rectangular coordinates

B)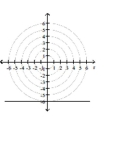

$y = - 6$ ; horizontal line 6 units
below the pole

C)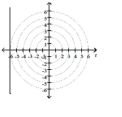

$x = - 6$ ; vertical line 6 units
to the left of the pole

D)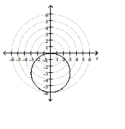

$x ^ { 2 } + ( y + 3 ) ^ { 2 } = 9$ ; circle, radius 3
center at $( 0 , - 3 )$ in rectangular coordinates