Multiple Choice
The graph of a piecewise-defined function is given. Write a definition for the function.
-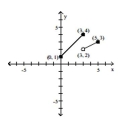 A)
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q1: The graph of a function is
Q2: The graph of a function f
Q3: Find the value for the function.<br>-
Q5: Match the correct function to the
Q6: The graph of a function is
Q7: Find the domain of the function.<br>-
Q8: Determine whether the relation represents a
Q9: Graph the function by starting with
Q10: Find and simplify the difference quotient
Q11: Graph the function by starting with