Multiple Choice
The graph of a piecewise-defined function is given. Write a definition for the function.
-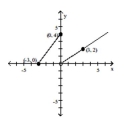 A)
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q115: Solve the problem.<br>-The amount of time it
Q154: Solve.<br>-The time in hours it takes a
Q169: Find the average rate of change
Q171: Use a graphing utility to graph
Q172: Find the value for the function.<br>-Find
Q175: Graph the function by starting with
Q177: Match the correct function to the
Q178: Graph the function by starting with
Q179: Find and simplify the difference quotient
Q274: Solve.<br>-The voltage across a resistor is jointly