Multiple Choice
Describe the transformations and give the equation for the graph.
-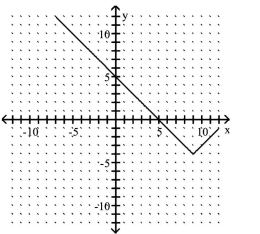
A) It is the graph of translated 9 units to the right and 4 units down. The equation is
B) It is the graph of translated 9 units to the right and 4 units down. The equation is
C) It is the graph of translated 9 units to the right and 4 units down. The equation is
D) It is the graph of translated 9 units to the right and 4 units down. The equation is
Correct Answer:

Verified
Correct Answer:
Verified
Q476: Find the center-radius form of the
Q477: Refer to the following graphs to
Q478: Evaluate the function.<br>-Find <span class="ql-formula"
Q479: Find the slope and the y-intercept
Q480: The graph of y = f(x)
Q482: Graph the function.<br>- <span class="ql-formula" data-value="f
Q483: Solve the problem.<br>-A deep sea diving bell
Q484: Choose the value which could represent
Q485: Find the average rate of change
Q486: Find the requested function value.<br>-Find