Multiple Choice
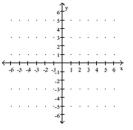
Decide whether the relation is a function.
- 
A) g shifts the graph of f vertically
up 3 units 
B) g shifts the graph of vertically
up 3 units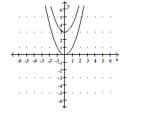
C) g shifts the graph of f vertically
down 3 units 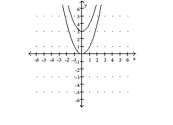
D) g shifts the graph of vertically
down 3 units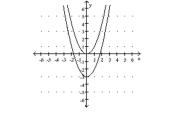
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q98: Use intercepts and a checkpoint to
Q99: Decide whether the relation is a function.<br>-{(-3,
Q100: Decide whether the relation is a function.<br>-Find
Q101: Find the domain of the function.<br>-
Q102: Rewrite the given equation in slope-intercept form
Q104: Use intercepts and a checkpoint to
Q105: Use the graph to find the indicated
Q106: The graph below shows the percentage of
Q107: Find the slope of the line
Q108: Graph the equation in the rectangular coordinate