Multiple Choice
Rewrite the given equation in slope-intercept form by solving for y.
- 
A) 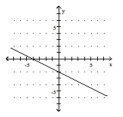
B) 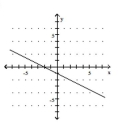
C) 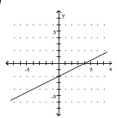
D) 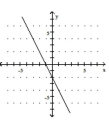
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q66: Find the domain and range.<br>-{(6,-6), (-4,7), (9,8),
Q67: Graph the equation in the rectangular
Q68: Use intercepts and a checkpoint to
Q69: Find the indicated function value.<br>- <span
Q70: Decide whether the relation is a
Q72: Decide whether the relation is a
Q73: Use the vertical line test to determine
Q74: Find the slope of the line
Q75: For the pair of functions, determine
Q76: Use the vertical line test to determine