Multiple Choice
Find the rule that defines each piecewise-defined function.
-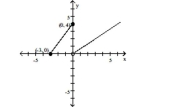
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q225: For the given functions f and
Q226: Use the vertical line test to determine
Q227: Find the domain of the composite
Q228: Use the horizontal line test to determine
Q229: Graph the function.<br>-f(x)= -2 <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7897/.jpg" alt="Graph
Q231: Use the vertical line test to determine
Q232: The graph of a function is given.
Q233: Use the graph to determine the
Q234: For the given functions f and
Q235: Graph the function by starting with