Provide an Appropriate Response Falling from Rest Under the Action of Gravity Encounters an Falling
Multiple Choice
Provide an appropriate response.
-If a body of mass falling from rest under the action of gravity encounters an air resistance proportional to three times the square root of velocity, then the body's velocity seconds into the fall satisfies the equation: where is a constant that depends on the body's aerodynamic properties and the density of the air.
Determine the equilibrium, velocity curve, and the terminal velocity for a skydiver with .
A) Equilibrium: 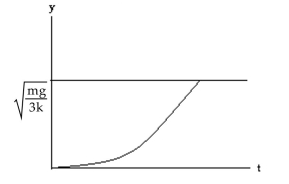
B) Equilibrium: 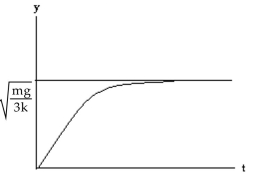
C) Equilibrium: 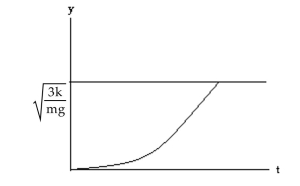
D) Equilibrium: 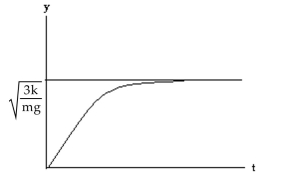
Correct Answer:

Verified
Correct Answer:
Verified
Q60: MULTIPLE CHOICE. Choose the one
Q61: Solve the initial value problem.<br>- <span
Q62: Show that the curves are orthogonal.<br>-
Q63: Solve the initial value problem.<br>- <span
Q64: MULTIPLE CHOICE. Choose the one
Q66: Use Euler's method to calculate the first
Q67: Solve the problem.<br>-The system of equations
Q68: MULTIPLE CHOICE. Choose the one
Q69: Obtain a slope field and add
Q70: Solve the problem.<br>-If the switch is