Find the Open Intervals on Which the Function Is Increasing

Multiple Choice

Find the open intervals on which the function is increasing and decreasing. Identify the function's local and absolute extreme values, if any, saying where they occur.
-

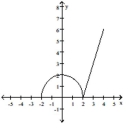
A) increasing on (-2, 0) and (2, 4) ; decreasing on (0, 2) ; absolute maximum at (4, 6) ; absolute minimum at (-2, 0) and (2, 0)
B) increasing on (2, 4) ; decreasing on (0, 2) ; absolute maximum at (4, 6) ; local maximum at (0, 2) ; absolute minimum at (-2, 0) and (2, 0)
C) increasing on (-2, 0) and (2, 4) ; decreasing on (0, 2) ; absolute maximum at (4, 6) ; local maximum at (0, 2) ; absolute minimum at (-2, 0) and (2, 0)
D) increasing on (-2, 0) and (2, 4) ; decreasing on (0, 2) ; absolute maximum at (4, 6) and(0,2) ; absolute minimum at (-2, 0) and (2, 0)