Multiple Choice
Sketch a typical level surface for the function.
-
A) 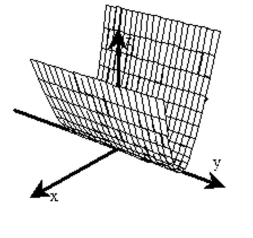
B) 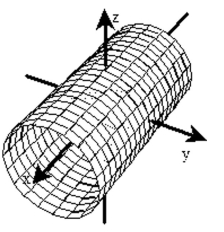
C) 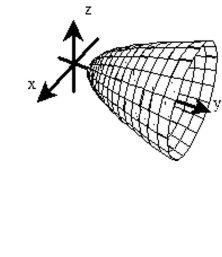
D) 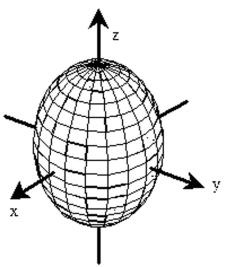
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q277: Use polar coordinates to find the
Q278: Provide an appropriate response.<br>-Find any local
Q279: Find the limit.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6591/.jpg" alt=" Find
Q280: Give an appropriate answer.<br>- <span class="ql-formula"
Q281: Find the absolute maxima and minima of
Q283: Solve the problem.<br>-The resistance <span
Q284: Solve the problem.<br>-The table below summarizes the
Q285: Solve the problem.<br>-Write an equation for the
Q286: Solve the problem.<br>- <span class="ql-formula" data-value="\text
Q287: Match the surface show below to the