Answer the Question $f ( x , y )$ (Thin Curves) as Well as the Constraint

Multiple Choice

Answer the question.
-The graph below shows the level curves of a differentiable function $f ( x , y )$ (thin curves) as well as the constraint $g ( x , y ) = \sqrt { x ^ { 2 } + y ^ { 2 } } - \frac { 3 } { 2 } = 0$ (thick circle) . Using the concepts of the orthogonal gradient theorem and the method of Lagrange multipliers, estimate the coordinates corresponding to the constrained extrema of 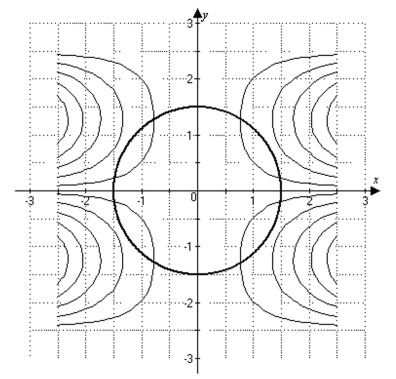$f ( x , y )$ .

A) (1.3, 0.7) , (-1.3, 0.7) , (-1.3,-0.7) , (1.3,-0.7)
B) (1.5, 0) , (0, 1.5) , (-1.5, 0) , (0, -1.5)
C) (1.1, 1.1) , (-1.1, 1.1) , (-1.1,-1.1) , (1.1,-1.1)
D) (1.5, 0.2) , (0.7, 1.3) , (-1.5, 0.2) , (-0.7, 1.3) , (-1.5, -0.2) , (-0.7, -1.3) , (1.5, -0.2) , (0.7, -1.3)