Solve the Problem $( 0 , \mathrm { p } )$

Multiple Choice

Solve the problem.
-A satellite dish is in the shape of a parabolic surface. Signals coming from a satellite strike the surface of the dish and are reflected to the focus, where the receiver is located. The satellite dish shown has a diameter of 10 feet and a depth of 7 feet. The parabola is positioned in a rectangular coordinate system with its vertex at the origin. The receiver should be placed at the focus $( 0 , \mathrm { p } )$ . The value of $\mathrm { p }$ is given by the equation $\mathrm { a } = \frac { 1 } { 4 \mathrm { p } }$ . How far from the base of the dish should the receiver be placed?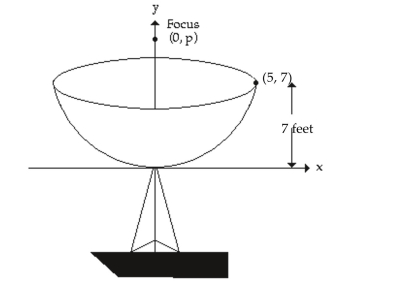

A) $\frac { 25 } { 28 }$ feet from the base
B) $3 \frac { 4 } { 7 }$ feet from the base
C) $\frac { 7 } { 25 }$ feet from the base
D) $1 \frac { 3 } { 25 }$ feet from the base