The Following Scatterplot Shows the Percentage of the Vote a Candidate

Multiple Choice

The following scatterplot shows the percentage of the vote a candidate received in the 2004 senatorial elections according to the voter's income level based on an exit poll of voters conducted by CNN. The income levels 1-8 correspond to the
Following income classes: 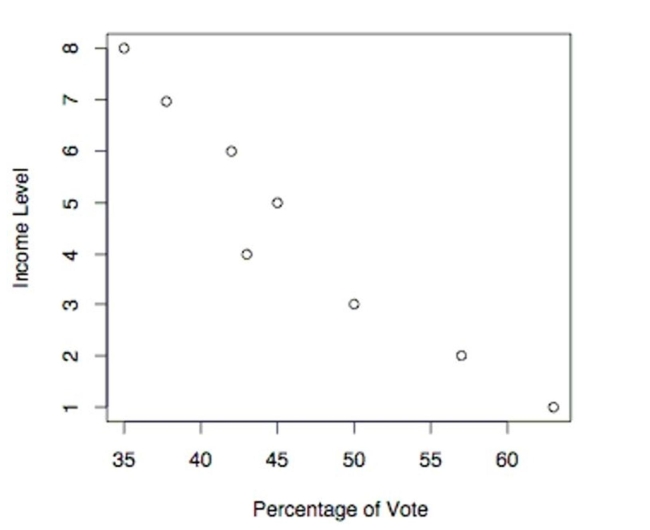$$\begin{array} { l } 1 = \text { Under } \$ 15,000 ; 2 = \$ 15 - 30,000 ; 3 = \$ 30 - 50,000 ; 4 = \$ 50 - 75,000 ; 5 = \$ 75 - 100,000 ; 6 = \$ 100 - 150,000 ; 7 = \\\$ 150 - 200,000 ; 8 = \$ 200,000 \text { or more. }\end{array}$$ Use the election scatterplot to determine whether there is a correlation between percentage of vote and income level at
The 0.01 significance level with a null hypothesis of $p _ { \mathrm { S } } = 0$

A) The test statistic is not between the critical values, so we reject the null hypothesis. There is sufficient evidence to support a claim of correlation between percentage of vote and income level.
B) The test statistic is between the critical values, so we fail to reject the null hypothesis. There is no evidence to support a claim of correlation between percentage of vote and income level.
C) The test statistic is between the critical values, so we reject the null hypothesis. There is sufficient evidence to support a claim of correlation between percentage of vote and income level.
D) The test statistic is not between the critical values, so we fail to reject the null hypothesis. There is no evidence to support a claim of correlation between percentage of vote and income level.