Short Answer
Evaluate the double integral
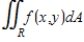
for the given function f(x, y) and the region R. Enter your answer as a fraction.
f(x, y) = 0x + 0y; R is bounded by x = 0,  , y = 0 and y = 4.
, y = 0 and y = 4.
Correct Answer:

Verified
Correct Answer:
Verified
Q134: Find the critical point(s) of the function.
Q135: Find the maximum and minimum values of
Q136: Find the critical point(s) of the function.
Q137: Evaluate the double integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Evaluate
Q138: Find the approximate change in z when
Q140: Find the volume of the solid bounded
Q141: An auxiliary electric power station will serve
Q142: Find the volume of the solid bounded
Q143: Maximize the function<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Maximize the
Q144: Evaluate the double integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg"