Solved

Find the Critical Point(s) of the Function

Question 134

Multiple Choice

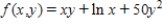
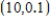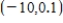Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) , are the critical points, the function has neither a relative maximum nor a relative minimum B) is the critical point, the function has neither a relative maximum nor a relative minimum C) is the critical point, the function has neither a relative maximum nor a relative minimum D) , are the critical points, the function has neither a relative maximum nor a relative minimum E) no critical points ​


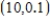A) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) , are the critical points, the function has neither a relative maximum nor a relative minimum B) is the critical point, the function has neither a relative maximum nor a relative minimum C) is the critical point, the function has neither a relative maximum nor a relative minimum D) , are the critical points, the function has neither a relative maximum nor a relative minimum E) no critical points , Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) , are the critical points, the function has neither a relative maximum nor a relative minimum B) is the critical point, the function has neither a relative maximum nor a relative minimum C) is the critical point, the function has neither a relative maximum nor a relative minimum D) , are the critical points, the function has neither a relative maximum nor a relative minimum E) no critical points are the critical points, the function has neither a relative maximum nor a relative minimum
B) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) , are the critical points, the function has neither a relative maximum nor a relative minimum B) is the critical point, the function has neither a relative maximum nor a relative minimum C) is the critical point, the function has neither a relative maximum nor a relative minimum D) , are the critical points, the function has neither a relative maximum nor a relative minimum E) no critical points is the critical point, the function has neither a relative maximum nor a relative minimum
C) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) , are the critical points, the function has neither a relative maximum nor a relative minimum B) is the critical point, the function has neither a relative maximum nor a relative minimum C) is the critical point, the function has neither a relative maximum nor a relative minimum D) , are the critical points, the function has neither a relative maximum nor a relative minimum E) no critical points is the critical point, the function has neither a relative maximum nor a relative minimum
D) Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) , are the critical points, the function has neither a relative maximum nor a relative minimum B) is the critical point, the function has neither a relative maximum nor a relative minimum C) is the critical point, the function has neither a relative maximum nor a relative minimum D) , are the critical points, the function has neither a relative maximum nor a relative minimum E) no critical points , Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. ​ ​ A) , are the critical points, the function has neither a relative maximum nor a relative minimum B) is the critical point, the function has neither a relative maximum nor a relative minimum C) is the critical point, the function has neither a relative maximum nor a relative minimum D) , are the critical points, the function has neither a relative maximum nor a relative minimum E) no critical points are the critical points, the function has neither a relative maximum nor a relative minimum
E) no critical points

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q129: Evaluate the double integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Evaluate

Q130: Sketch the domain of the function. ​

Q131: Maximize the function ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Maximize

Q132: Find the first partial derivatives of the

Q133: Maximize the function ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Maximize

Q135: Find the maximum and minimum values of

Q136: Find the critical point(s) of the function.

Q137: Evaluate the double integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Evaluate

Q138: ​Find the approximate change in z when

Q139: Evaluate the double integral<br>​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Evaluate