Multiple Choice
Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 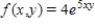
A) 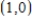 ; relative maximum value:
; relative maximum value: 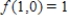
B)  ; relative minimum value:
; relative minimum value: 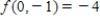
C)  ; saddle point:
; saddle point: 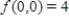
D) there are no critical points
Correct Answer:

Verified
Correct Answer:
Verified
Q209: The flow of blood through an arteriole
Q210: Find the total differential of the function.<br>
Q211: Use a double integral to find the
Q212: Use a double integral to find the
Q213: Find the total differential of the function.
Q214: Find the total differential of the function.
Q215: Maximize the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Maximize
Q216: Find the first partial derivatives of the
Q217: The Country Workshop's total weekly profit (in
Q218: Find the maximum and minimum values of