Short Answer
Consider the function 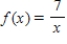 at
at 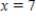 .
.
Find the Taylor series of the function at the indicated point.
__________
Find its radius of convergence.
__________
Find the interval of convergence.
__________
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Use the Newton method to approximate the
Q3: Consider the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Consider the
Q4: Show that the series is divergent. <img
Q5: Find P<sub>3</sub>(x), the third Taylor polynomial of
Q6: Consider the series<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Consider the
Q7: Consider the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Consider the
Q8: Estimate the value of the radical by
Q9: Use the sixth-degree Taylor polynomial to approximate<br>
Q10: Estimate the value of the radical by
Q11: Consider the series<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Consider the