Short Answer
Use the Newton method to approximate the indicated zero of the function. Continue with the iteration until two successive approximations differ by less than 0.0001. Round your answer to five decimal places, if necessary.
The zero of 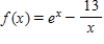 between
between 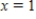 and
and  ,
,  .
.
Correct Answer:

Verified
Correct Answer:
Verified
Q2: Consider the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Consider the
Q3: Consider the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Consider the
Q4: Show that the series is divergent. <img
Q5: Find P<sub>3</sub>(x), the third Taylor polynomial of
Q6: Consider the series<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Consider the
Q7: Consider the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Consider the
Q8: Estimate the value of the radical by
Q9: Use the sixth-degree Taylor polynomial to approximate<br>
Q10: Estimate the value of the radical by
Q11: Consider the series<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8255/.jpg" alt="Consider the