A Lake with Constant Volume V, in Km³, Contains a Quantity

Short Answer

A lake with constant volume V, in km³, contains a quantity of Q km³ pollutant. Clean water enters the lake and causes a total outflow of r km³ per year. The rate at which the pollutant decreases at any time t equals the product of the pollutant Q per volume V and the rate at which the water flows out of the lake. If 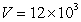km³ and 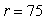km³ per year, how many years will it take for the pollutant to decrease to half of its original quantity? Round to the nearest whole year.