On January 1, 1879, Records Show That 500 of a Fish

Multiple Choice

On January 1, 1879, records show that 500 of a fish called Atlantic striped bass were introduced into the San Francisco Bay. In 1899, the first year fishing for bass was allowed, 100,000 of these bass were caught, representing 10% of the population at the start of 1899. Owing to reproduction, at any time the bass population is growing at a rate proportional to the population at that moment. Assume that when fishing starts in 1899, the rate at which bass are caught is proportional to the square of the population with constant of proportionality 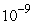. What happens to the bass population in the long run?

A) It approaches 0.
B) It grows without bound.
C) It approaches .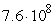
D) It approaches .