A Sample of 100 Colored Balls Is Selected from a Large

Multiple Choice

A sample of 100 colored balls is selected from a large container of red balls and white balls-call it Container A.A second sample, this one of size 200, is selected from another container of red balls and white balls-call it Container B.The table below shows observed results from the two samples. 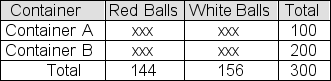You plan to use a chi-square test to test the null hypothesis that the two containers contain the same proportion of red balls.The significance level for the test will be 1%.Suppose the p-value for the sample result turns out to be .0272.What should you conclude?

A) At a 1% significance level, don't reject the hypothesis that the proportion of red balls is the same in both containers.
B) At a 1% significance level, reject the hypothesis that the proportion of red balls is the same in both containers.
C) The test provides strong evidence that the proportion of red balls is not the same in both containers.
D) The test provides strong evidence that the proportion of red balls is the same in both containers.