Solved

Use Lagrange Multipliers to Find the Maximum Value of

Question 8

Multiple Choice

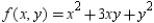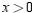Use Lagrange multipliers to find the maximum value of Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​ where Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​ and Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​ subject to the constraint Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​ . ​


A) maxima: Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​ ; minima: Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​
​
B) maxima: Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​ ; minima: Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​
​
C) maxima: Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​ ; minima: Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​
​
D) maxima: Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​ ; minima: Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​
​
E) maxima: Use Lagrange multipliers to find the maximum value of where and subject to the constraint . ​ A) maxima: ; minima: ​ B) maxima: ; minima: ​ C) maxima: ; minima: ​ D) maxima: ; minima: ​ E) maxima: ; minima: ​ ; minima: Use Lagrange multipliers to find the maximum value of where and 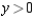subject to the constraint 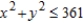. ​ A) maxima: 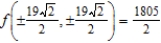; minima: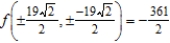 ​ B) maxima: 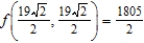; minima: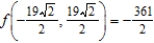 ​ C) maxima: 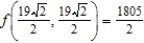; minima: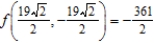 ​ D) maxima: 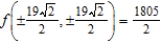; minima: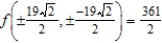 ​ E) maxima: 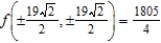; minima: ​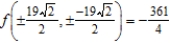
​

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q3: Find a unit normal vector to the

Q4: Find the second partial derivative for the

Q5: Use Lagrange multipliers to minimize the function

Q6: Find symmetric equations of the normal line

Q7: Examine the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Examine the

Q9: Determine the continuity of the function <img

Q10: Find the critical points of the function

Q11: For <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="For ,

Q12: ​Find the partial derivative <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="​Find

Q13: Find the maximum value of the directional