Solved

Use Lagrange Multipliers to Minimize the Function Subject to the Following

Question 5

Multiple Choice

Use Lagrange multipliers to minimize the function Use Lagrange multipliers to minimize the function subject to the following two constraints. Assume that x, y, and z are nonnegative. A) B) C) D) E) subject to the following two constraints. Use Lagrange multipliers to minimize the function subject to the following two constraints. Assume that x, y, and z are nonnegative. A) B) C) D) E) Use Lagrange multipliers to minimize the function subject to the following two constraints. Assume that x, y, and z are nonnegative. A) B) C) D) E) Assume that x, y, and z are nonnegative.


A) Use Lagrange multipliers to minimize the function subject to the following two constraints. Assume that x, y, and z are nonnegative. A) B) C) D) E)
B) Use Lagrange multipliers to minimize the function subject to the following two constraints. Assume that x, y, and z are nonnegative. A) B) C) D) E)
C) Use Lagrange multipliers to minimize the function subject to the following two constraints. Assume that x, y, and z are nonnegative. A) B) C) D) E)
D) Use Lagrange multipliers to minimize the function subject to the following two constraints. Assume that x, y, and z are nonnegative. A) B) C) D) E)
E) Use Lagrange multipliers to minimize the function 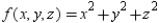subject to the following two constraints.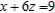 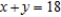Assume that x, y, and z are nonnegative. A) 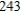B) 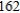C) 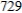D) 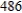E)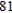

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find using

Q2: Use Lagrange multipliers to find the minimum

Q3: Find a unit normal vector to the

Q4: Find the second partial derivative for the

Q6: Find symmetric equations of the normal line

Q7: Examine the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Examine the

Q8: Use Lagrange multipliers to find the maximum

Q9: Determine the continuity of the function <img

Q10: Find the critical points of the function

Q11: For <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="For ,