Solved

Solve the Inequality and Draw a Number Line Graph of the Solution

Question 216

Multiple Choice

Solve the inequality and draw a number line graph of the solution.
- 3(1+x) +4(1−x) <x+23 ( 1 + x ) + 4 ( 1 - x ) < x + 2
Solve the inequality and draw a number line graph of the solution. - 3 ( 1 + x ) + 4 ( 1 - x ) < x + 2 A) B) C) D)


A)
Solve the inequality and draw a number line graph of the solution. - 3 ( 1 + x ) + 4 ( 1 - x ) < x + 2 A) B) C) D)
B)
Solve the inequality and draw a number line graph of the solution. - 3 ( 1 + x ) + 4 ( 1 - x ) < x + 2 A) B) C) D)
C)
Solve the inequality and draw a number line graph of the solution. - 3 ( 1 + x ) + 4 ( 1 - x ) < x + 2 A) B) C) D)
D)
Solve the inequality and draw a number line graph of the solution. - 3 ( 1 + x ) + 4 ( 1 - x ) < x + 2 A) B) C) 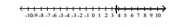D)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q211: Solve the inequality graphically.<br>- <span class="ql-formula"

Q212: Use words to describe the interval

Q213: Find the value of x and

Q214: Write the sum or difference in the

Q215: Draw a scatter plot of the data

Q217: Evaluate the expression.<br>- <span class="ql-formula" data-value="|

Q218: Solve the equation using the quadratic

Q219: Find the midpoint of the line

Q220: Solve by completing the square.<br>- <span

Q221: Find a point-slope form equation for