A 95% Confidence Interval Estimate of the Population Mean μ

Multiple Choice

A 95% confidence interval estimate of the population mean μ can be interpreted to mean that:

A) if we repeatedly draw samples of the same size from the same population, 95% of the values of the sample means will result in a confidence interval that includes the population mean μ.
B) there is a 95% probability that the population mean μ will lie between the lower interval limit and the upper interval limit.
C) we are 95% confident that we have selected a sample whose range of values does not contain the population mean μ.
D) we are 95% confident that 5% of the values of the sample means 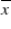will result in a confidence interval that includes the population mean μ.